1.2.1 二进制数
二进制系统中的两个数——1和0,称为位(比特,bit),是二进制数(binary digit)的缩写.在数字电路中,使用两个不同的电压电平表示这两个位.一般情况下,高电压用1来表示,低电压用0来表示.这称为正逻辑,本书将都使用正逻辑. $$ 高电压(H)=1低电压(L)=0 $$ 在另一种系统中,1表示低电压,0表示高电压,这称为负逻辑. 一组位(一些1和0的组合)称为码,用来表示数字,字母,符号,指令及任何给定应用中的对象.
1.2.2 逻辑电平
用来表示1和0的电压称为逻辑电平.理想情况下,一个电平表示高电压,另一个电平表示低电压.在实际的数字电路中,这个高电压可以是指定的最小值和最大值之间的任意值.同样,低电压也可以是指定的最小值和最大值之间的任意值.在指定的高电平范围和低电平范围之间是不能有重叠的.
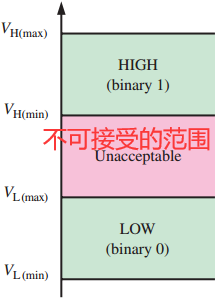
图1.5给出了数字电路中高电平和低电平的通常范围.变量 $V_{H(max)}$ 表示高电平的最大值,变量 $V_{H(min)}$ 表示高电平的最小值.$V_{L(max)}$ 表示低电平的最大值,$V_{L(min)}$ 表示低电平的最小值.在正常的工作情况下,$V_{L(max)}$ 和 $V_{H(min)}$ 之间的电压值是不可以出现的.对于一个给定的电路,在此范围内的电压既可以是高电平,也可以是低电平.例如,在CMOS 数字电路中,高电平值在2~3.3 V,低电平压值在0~0.8 V,也就是说,如果使用2.5 V,电路将把它看成是高电平或二进制1.如果使用0.5 V,那么就是低电平或二进制0.对于这种类型的电路,0.8~2 V的电平值是不可以出现的.
1.2.3 数字波形
数字波形由两种不同的电平值组合而成,它们在高,低电平或状态之间不断地变化.图1.6(a)给出一个正向脉冲,是在电压(或电流)从低电平变到高电平,再从高电平变回到低电平时产生的.图1.6(b)给出一个反向脉冲,是在电压从高电平变到低电平,再从低电平变回到高电平时产生的.数字波形由这一系列的脉冲组成.

脉冲 如图1.6所示,脉冲有两个边沿:在t时刻首先出现的为前沿,在t,时刻随后出现的为后沿.对于一个正向脉冲,前沿是上升沿,后沿是下降沿.图1.6所示的脉冲是理想状态下的脉冲,因为假设上升沿和下降沿的变化是没有时间范围的(瞬间).实际情况是,这些变化是有时间范围的,尽管大多数的数字波形可以假定为理想脉冲.
图1.7给出了一个非理想的脉冲.实际上,所有脉冲或多或少都存在这些非理想的特性.通常,杂散电感和电容效应会产生超调量和振荡.杂散电容和电路电阻会产生下调量,形成时间常数不大的RC电路.
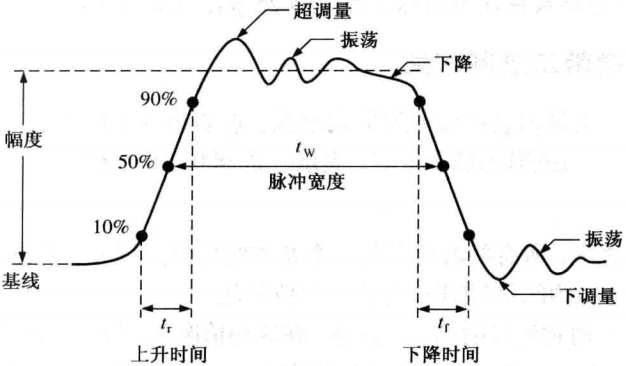 $$
图1.7非理想脉冲的特性
$$
$$
图1.7非理想脉冲的特性
$$
从低电平到高电平所需的时间称为上升时间t,,从高电平到低电平所需的时间称为下降时间t.在实际运用中,通常测量的上升时间是从脉冲幅度(相对于基线的高度)的10%处到脉冲幅度的90%处的时间宽度,测量的下降时间则是从幅度的90%处到幅度的10%处的时间宽度.如图1.7所示,上升时间和下降时间不包括脉冲顶部和底部的10% ,因为这部分区域的波形是非线性的.脉冲的宽度tw就是脉冲的持续时间,通常把上升沿和下降沿幅度50%处的时间间隔定义为脉冲宽度,如图1.7所示.
波形特性 在数字系统里,遇到的大多数波形都是由一系列的脉冲组成的,有时称为脉冲序列,它们可以分为周期的和非周期的.周期波形就是在一个固定的时间间隔里不断重复自身,这个时间间隔称为周期( $T$ ).频率( $f$ )是重复的速率,测量单位是赫兹( $Hz$ ).而一个非周期性脉冲波形则不会在一个固定的时间间隔里重复,它可能由脉冲宽度不确定的脉冲组成,也有可能由时间间隔不确定的脉冲组成,图1.8给出两种波形的例子.
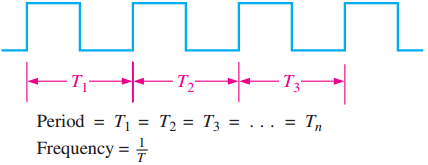 $$
(a)周期(方波)
$$
$$
(a)周期(方波)
$$
 $$
(b)非周期
$$
脉冲(数字)波形的频率(f)就是其周期(T)的倒数,它们之间的关系如下所示:
$$
(1.1) f = \frac{1}{T}
$$
$$
(1.2) T = \frac{1}{f}
$$
周期数字波形的一个重要特性就是它的占空比,它是脉冲宽度( $t_w$ )和周期( $T$ )的比值,可以用百分比来表示
$$
(1.3)占空比=(\frac{t_w}{T})×100\%
$$
$$
(b)非周期
$$
脉冲(数字)波形的频率(f)就是其周期(T)的倒数,它们之间的关系如下所示:
$$
(1.1) f = \frac{1}{T}
$$
$$
(1.2) T = \frac{1}{f}
$$
周期数字波形的一个重要特性就是它的占空比,它是脉冲宽度( $t_w$ )和周期( $T$ )的比值,可以用百分比来表示
$$
(1.3)占空比=(\frac{t_w}{T})×100\%
$$
1.2.4 数字波形携带二进制信息
数字系统处理的二进制信息以波形的形式出现,它表示顺序序列的二进制位.当波形为高电平时,表示二进制1;当波形为低电平时,表示二进制0.每个位在一个序列里所占的固定时间间隔称为位时间.
时钟 在数字系统中,所有的波形都与一个基本时序波形同步,称之为时钟( clock).时钟是周期波,每个脉冲之间的间隔(周期)等于一个位时间.
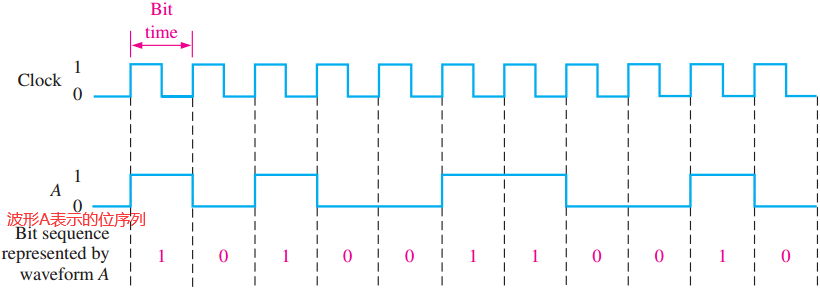 $$
图1.10时钟波形和位序列表示的波形同步的例子
$$
图1.10所示为一个时钟波形的例子.注意,在这种情况下,波形A的电平变化都发生在时钟波形的前沿.在其他情况下,电平的变化发生在时钟的后沿.在每个位时间之内,波形A可为高电平也可为低电平.这些高电平和低电平组成了图1.10所示的位序列.若干位组成—组就可作为一个二进制信息来使用,如表示数字或字母.而时钟波形本身并不携带任何信息.
$$
图1.10时钟波形和位序列表示的波形同步的例子
$$
图1.10所示为一个时钟波形的例子.注意,在这种情况下,波形A的电平变化都发生在时钟波形的前沿.在其他情况下,电平的变化发生在时钟的后沿.在每个位时间之内,波形A可为高电平也可为低电平.这些高电平和低电平组成了图1.10所示的位序列.若干位组成—组就可作为一个二进制信息来使用,如表示数字或字母.而时钟波形本身并不携带任何信息.
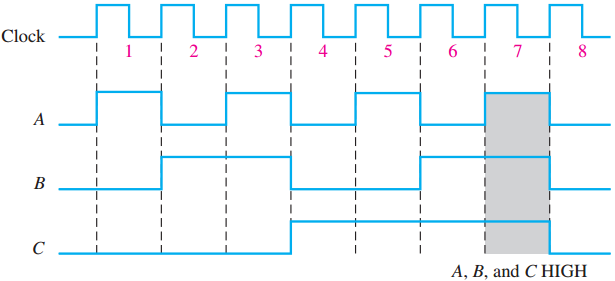 时序图时序图就是数字波形的图形,它表示两个或两个以上波形的实际时间关系,还表示波形和波形之间的相互变化关系.图1.11给出了4个波形组成的时序图的例子.从这个时序图可以确定相互关系.例如,波形A,B和C仅在位时间7时同为高电平(阴影部分),在位时间7结束时变回到低电平.
时序图时序图就是数字波形的图形,它表示两个或两个以上波形的实际时间关系,还表示波形和波形之间的相互变化关系.图1.11给出了4个波形组成的时序图的例子.从这个时序图可以确定相互关系.例如,波形A,B和C仅在位时间7时同为高电平(阴影部分),在位时间7结束时变回到低电平.
1.2.5 数据传送
数据是指一组可以用来传递某种信息的位.使用数字波形表示的二进制数据,必须在数字系统中从一个电路传送到另一个电路,或者从一个系统传送到另一个系统,以实现某个设定的目的.例如,计算机存储器中的数字是以二进制的形式存储的,它必须传送到计算机的中央处理器才能实现加法运算.然后加法运算的结果必须传送到显示器显示并且/或者回送到存储器中.如图1.12所示,二进制数据的传送方式有两种——串行和并行.
 $$
(a)从计算机到调制解调器串行传送8位二进制数据.第一个间隔为 t_0 到 t_1
$$
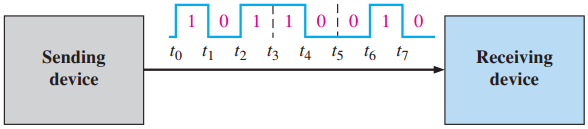
图1.12(a)为计算机传送数据到调制解调器的例子,这时位以串行的方式从一个点传送到另一个点,沿着一条导线每次传送一位.在 $t_0$ 到 $t_1$这段时间间隔里,送出第一位.在 $t_1$ 到 $t_2$ 这段时间间隔里,送出第二位,以此类推.若要串行输出8位,则需花费8个时间间隔.
$$
(a)从计算机到调制解调器串行传送8位二进制数据.第一个间隔为 t_0 到 t_1
$$
图1.12(a)为计算机传送数据到调制解调器的例子,这时位以串行的方式从一个点传送到另一个点,沿着一条导线每次传送一位.在 $t_0$ 到 $t_1$这段时间间隔里,送出第一位.在 $t_1$ 到 $t_2$ 这段时间间隔里,送出第二位,以此类推.若要串行输出8位,则需花费8个时间间隔.
 $$
(b)从计算机到打印机并行传送8位
二进制数据.开始时间为t_0
$$
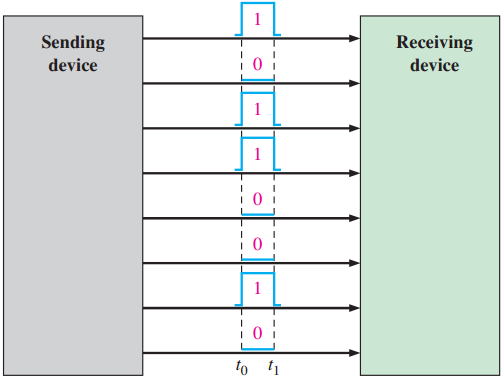
当若干位以并行的方式传送时,一组位中的每一个位可以同时通过不同的线路传送.图1.12(b)为8位数据从计算机传送到打印机的例子.和串行传送需要8个时间间隔相比,并行方式传送8个位只需要一个时间间隔.
$$
(b)从计算机到打印机并行传送8位
二进制数据.开始时间为t_0
$$
当若干位以并行的方式传送时,一组位中的每一个位可以同时通过不同的线路传送.图1.12(b)为8位数据从计算机传送到打印机的例子.和串行传送需要8个时间间隔相比,并行方式传送8个位只需要一个时间间隔.
综上所述,二进制数据串行传送的优点是所需要的数据线最少,即只需要一条线路.而在并行传送中,线路的数量等于一次传送的位的数量.串行传送的缺点是相对于并行传送,它需要更长的时间来完成一个给定位数的传送.例如,如果1 us可以传送一位,那么需8 us来完成串行传送8个位,但并行传送8个位只需1 us.并行传送的缺点是和串行相比,需要更多的线路