2.11.1格雷码
格雷(Gray)码是无权码,并不是算术编码;也就是没有赋予不同位的特足的权.恰雷俏的重要特征是,从一个码字到下一个接续码字仅有一位发生了变化.这个特征在许多应用程序中是非常重要的,例如对于轴位编码器,在两个相邻顺序数之间,错误敏感度随着位数改变数目的增加而增加.
- ◇ 格雷码的一位改变的特征减小了出错概率.
表2.6列出了十进制数 0~15 所对应的 4 位格雷码,表中给出了二进制数以做参照.和二进制数相似,格雷码可以拥有任意的位数.注意两个相邻的格雷码字之间的一位变化.例如,从十进制数 3 到十进制数 4,格雷码从 0010 变为 0110,而二进制编码从 0011 变为 0100 改变了 3 个位.格雷码中唯一的位改变是从右数的第 3 位,其他位保持不变. $$ 表2.6 ~~~4位格雷码 $$
| 10进制 | 2进制 | 格雷码 |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
二进制数到格雷码的转换 二进制数和格雷码之间的转换有时很有用.下面的规则解释了怎样把二进制数变换为格雷码.
- 格雷码中的最高有效位(最左边)等同于二进制数中相应的最高有效位.
- 从左到右,加上每一对相邻的二进制编码位,得到下一个格雷码位.舍去进位.
例如,二进制数 10110 到格雷码的转换如下:
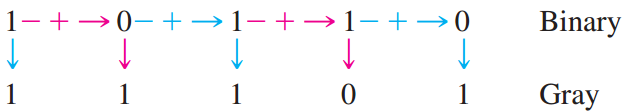
格雷码为11101.
格雷码到二进制数的转换 为了把格雷码转为二进制数,可以使用相似的方法,但是有一些区别.可以应用下面的规则.
- 二进制编码中的最高有效位(最左边)等于格雷码中相应的位.
- 将所产生的每个二进制编码位加上下一相邻位置的格雷码位.舍去进位.
例如,格雷码 11011 到二进制的转换如下:
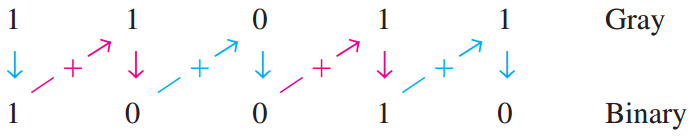
二进制数是10010.
2.11.2典型应用
3 位轴位编码器的示意图如图2.6所示.通常,有三个同心圆环被分成 8 个扇区.扇区越多,位置就能表示得越准确,但是为了解释的方便,仅仅使用了 8 个扇区.每个圆环的每个扇区分为能够反射光束或不能反射光束两种,当圆环随着轴转动时,处于红外线(IR)发射器下部的扇区分别接收红外线发射器所产生的 3 条光束.当扇区反射光束时表示 1,当扇区不反射光束时表示 0.红外线探测器检测是否存在反射光束,然后产生相应的 3 位编码.红外线发射器/探测器处于固定位置,当轴逆时针 360° 旋转时, 8 个扇区在3条光束下移动.每一条光束被扇区的表面反射或吸收,产生表示轴位编码器位置的二进制数或格雷码.
在图2.6(a)中,这些扇区直接以二进制格式排列,所以探测器输出从 000 到001,再到 010,再到 011,等等.当光束处于反射扇区上部时,输出为 1;当光束处于非反射扇区上部时,输出为 0.如果从一个扇区到另一个扇区的转换瞬间,一条光束稍微先于其他光束被反射或吸收,就会产生一个错误的输出.考虑这 3 条光束从 111 扇区变换到 000 扇区所发生的情况.如果最高位的光束略微超前,那么由于 111 或 000 被 011 瞬间替代,轴位将被错误地显示.在这个应用中,要使得红外发射器/探测器的安装精确对齐,实际上是不可能的,因此在扇区之间瞬间变换时,通常会发生错误.
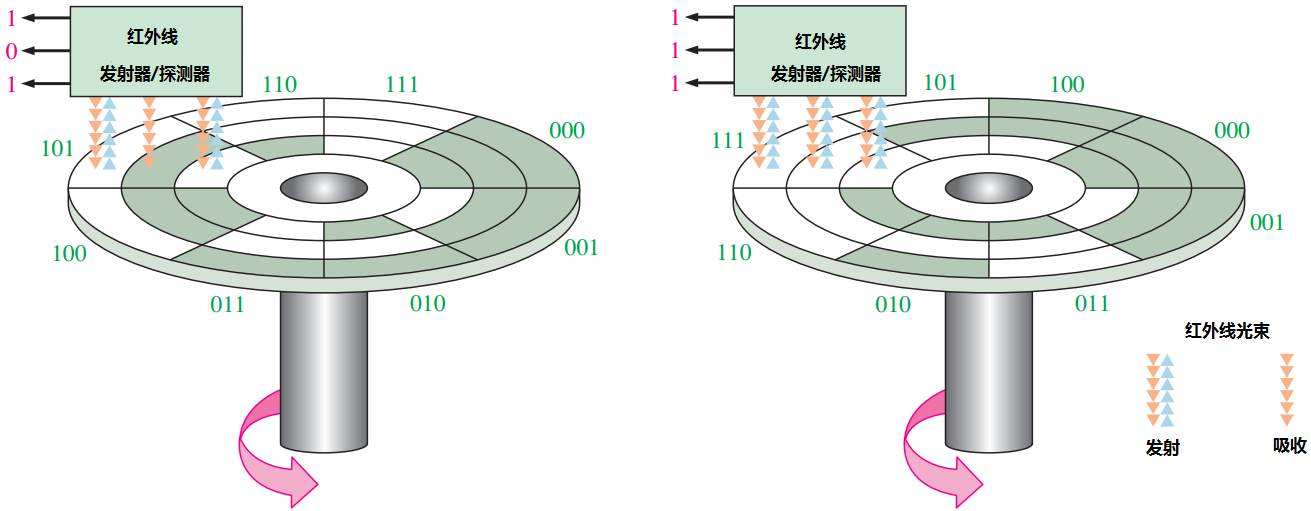$$
(a)二进制码~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(b)格雷码
$$
$$
图2.6一个简单的例子,解释在轴位编码器中格雷码是如何解决出错问题的.虽然大多数
\\
轴位编码器使用10位以上的编码以提高分辨率,但是使用3位就可以解释这种概念
$$
格雷码用来消除二进制所固有的这类出错问题.如图2.6(b)所示,格雷码保证了在两个相邻的扇区中,只有一个位会发生改变.这就意味着即使光束没有精确对准,也绝对不会发生转移瞬间中的错误.例如,再一次考虑,当光束位于 111 扇区,准备进入下一个 101 扇区会发生什么情况.无论光束是否对准,在转移瞬间只有两个可能的输出 111 和 101.在其他扇区的转移瞬间中,也会产生相同的结果.