2.3.1 权和的方法
◇ 如果要把一个已知的十进制数转换为二进制数,只要求出二进制数的权,全部权加起来就是十进制数.
想要得到一个给定十进制数的二进制数,只要确定二进制数权的和,它们等于相应的十进制数.记住二进制权的简单方法是最低位为1,也就是$2^0$,任何一个权乘以2,就会得到下一个更高位的权,因此7个二进制权的序列就是64,32,16,8,4,2,l,这和上一节学到的一样.例如,十进制数9就可以由二进制权的和表示如下: $$ 9=8+1或者9=2^3+2^0 $$ 把1放在适当的权的位置上,即 $2^3$ 和 $2^0$,把0放在 $2^2$ 和 $2^1$ 的位置上,就确定了十进制数9.
| 2^3 | 2^2 | 2^1 | 2^0 |
|---|---|---|---|
| 1 | 0 | 0 | 1 |
十进制数9的二进制数表达
2.3.2 重复除以2的方法
◇要得到一个给定十进制数的二进制数,可以用2除这个十进制数直至商为0,每次余数的全部便构成了二进制数.
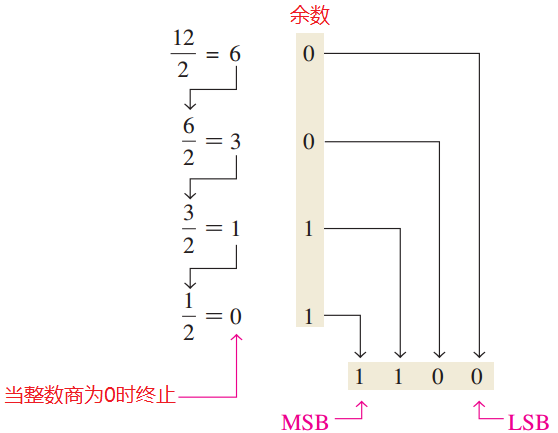
将十进制整数转换为二进制数的系统方法是重复除以2的过程.例如,把十进制数12转换为二进制数,首先12除以2.然后把每次得到的商都除以2,直到商为0.每次相除所得到的余数就构成了二进制数.第一个得到的余数是二进制数中的最低有效位(ISB),最后一个产生的余数是最高有效位(MSB).将十进制数12转换为二进制数的过程由下列步骤给出.
2.3.3 十进制小数转换为二进制数
例2.5和例2.6给出了整数的转换,现在来看小数的转换.记住小数二进制权的一个简单的方法是最高有效权是0.5,也就是$2^{-1}$,任何一个权除以2,就得到次低位的权;因此4个小数的二进制权的序列就是0.5, 0.25, 0.125,0.0625.
权和 权和的方法可以应用于十进制小数,如以下的例子所示: $$ 0.625= 0.5 +0.125 = 2^{-1} + 2^{-3} =0.101 $$
在$2^{-1}$位置上有一个1,在 $2^{-2}$ 位置上有一个0,而在$2^{-3}$位置上有一个1.
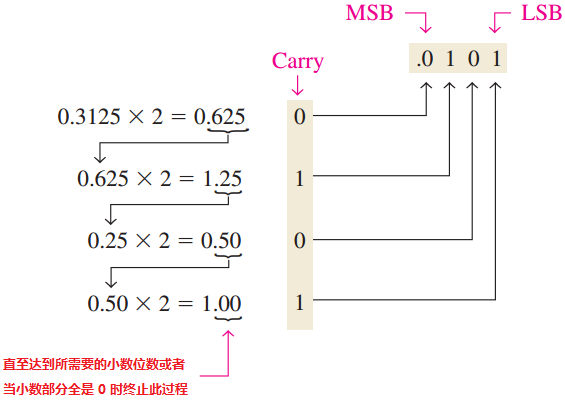
重复乘2 正如所见,可以用重复除以 2 的方法把十进制整数转换为二进制数.二进制小数则可以用重复乘2的方法转换得到.例如,把十进制小数 0.3125 转换为二进制数,首先把 0.3125 乘以 2,然后把每次乘积的小数部分乘以 2,直到乘积的小数部分为 0,或者达到了所需要的小数位数. 由相乘产生的进位数字或者进位,就生成了二进制数. 所产生的第一个进位是最高有效位(MSB),最后一个进位是最低有效位(LSB).该过程如下所示: