2.4.1 二进制加法
◇ 在二进制中,1+1 = 10,而不是2.
二进制数(位)加法的 4 条基本规则如下:
| 0+0=0 和为0. 进位是0 |
|---|
| 0+1=1 和为1. 进位是0 |
| 1+0=1 和为1. 进位是0 |
| 1+1=10 和为10. 进位是1 |
注意: 前三条规则产生单个的位,而在第4条规则中,两个1相加生成二进制的2(10).二进制数在相加时,最后一种情况在低位的和为0,而在左边的高位产生了进位1,如下面的加法运算 11+1 所示:
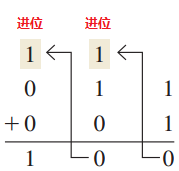在最右列中,1+1=0,因而在此列的左侧一列,即中间一列产生进位1.在中间一列中,1+1+0=0,因而在此列的左侧一列中产生进位1.在最左列中,1+0+0 =1.
当存在进位1时,就会遇到三个位进行加法的情况(两个数中的位和一个进位).这种情况如下所示:
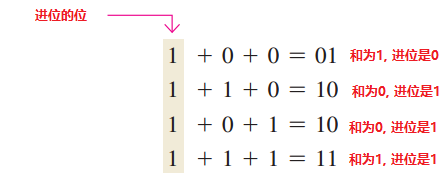
2.4.2 二进制减法
◇ 在二进制中,10 - 1 =1,而不是9.
二进制数(位)减法的4条基本规则如下:
| 0-0=0 |
| 1-1=0 |
| 1-0=1 |
| 10-1=1 0-1 产生借位1 |
进行减法运算时,有时必须从左边一列中借位.在二进制中,仅当0减去1时才需要借位.在这种情况下﹐从左边一列借来1,被减的列就会出现10,这时必须使用上面列出的4条基本规则中的最后一条.例2.8和例2.9说明了二进制减法,同时也给出了相应的十进制减法.
2.4.3 二进制乘法
◇ 两位的二进制乘法和十进制数О和1的乘法相同.
位相乘的4条基本规则如下:
| 0 * 0 = 0 |
| 1 * 1 = 0 |
| 1 * 0 = 1 |
| 10 * 1 = 1 ~~ 0 - 1 产生借位1 |
二进制乘法和十进制乘法的运算方法是一样的.这涉及部分积的形成,把相继的部分积向左移一位,然后把所有的部分积加起来.例2.10说明了这个过程,同时也给出了相应的十进制乘法作为参照.
2.4.4 二进制除法
一个计数器可以用来进行二进制的算术运算,只要不超出计数器的运算范围.
二进制中的除法遵循和十进制除法一样的过程, 如例2. 11所示,其中给出了相应的十进制除法.