2.6.1 符号位
二进制符号数的最左边就是符号位,指出这个数是正数还是负数.符号位 0 表示正数,1 表示负数.
2.6.2 符号数值的形式
当以符号数值的形式表示带符号二进制数时,最左边的一位是符号位,其余的都是数值位.数值位对于正数和负数来说都是二进制原码(非补码).例如,十进制数+25表示为符号数值的形式就是一个 8 位带符号二进制数,使用符号数值的形式为
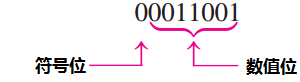
十进制数-25表示为 $$ 10011001 $$ 注意 +25 和 –25 之间的唯一区别是符号位,因为对于正数和负数来说,数值位都是二进制原码.
在符号数值的形式中,负数和其相应的正数具有相同的数值位,但其符号位为 1 而不是 0.
2.6.3 反码形式
以反码形式表示正数的方法和以符号数值形式表示正数的方法是一致的.但是,负数却是其相应正数的反码.例如,使用 8 位数字,十进制数 -25 可以表示为 +25(00011001) 的反码 $$ 11100110 $$ 在反码形式中,负数就是其相应正数的反码.
2.6.4 补码形式
正数的补码形式表示方法和符号数值与反码形式的表示方法是一致的.负数是相应正数的补码.再次使用 8 位数字,把十进制数 -25 表示为 +25(000011001) 的补码.按位取反再加 1,得到 $$ -25 =11100111 $$ 在补码形式中,负数是相应正数的补码.
2.6.5 带符号数的十进制值
符号数值 在符号数值的形式中,正数和负数的十进制值,是由所有数值位为 1 的相应权加起来得到的,不考虑那些为 0 的位.符号通过检查符号位来确定.
反码 在反码形式中,正数的十进制值是由所有为 1 的数值位相应的权加起来得到的,而不要考虑为 0 的位置.负数的十进制值是通过给符号位的权赋以负值,并把所有为 1 的数值位相应的权加起来再加上 1 得到的.
补码 在补码形式中,正数和负数的十进制值,是把所有为 1 的数值位相应的权加起来得到的,而不要考虑为 0 的位置.负数中符号位的权被赋予负值.
从这些例子中,可以看到为什么用补码形式来表示带符号整数比较好: 在转换为十进制数时,仅仅需要求权的和,而不用考虑是正数还是负数.对于负数而不是正数,反码形式需要给权的和再加上 1.当然反码形式并不是常用的,因为 0 的反码有两种可能的表示方式(00000000或11111111).
2.6.6 带符号整数的表示范围
◇ 二进制数的数值范围取决于数的位数(n).
使用 8 位数给出说明,因为在大多数计算机中通常使用 8 位的组合,并被赋予特殊的名称,即字节(byte).使用一个字节或者 8位,可以表达 256 个不同的数.使用两个字节或者 16 位,可以表达 65536 个不同的数.使用 4 个字节或者 32 位,可以表达 $4.295 * 10^9$ 个不同的数.求解 n 位的不同组合个数的公式是 $$ 总组合数=2^n $$ 对于补码带符号数,n 位数的数值范围是 $$ -(2^{n-1})到+(2^{n-1} -1) $$ 其中对于每一个数,都有一个符号位和 n-1 个数字位.例如,使用 4 位数,并以补码表示的数的范围是从 $–(2^3) =-8$到$2^3-1 = +7$.类似地,利用 8 位,就可以从 –128 到 +127; 使用 16 位,就可以从 – 32 768 到 +32 767;等等.
2.6.7 浮点数
为了表示很大的整数,就会需要多个位.当需要表示的数值同时具有整数和小数部分时(比如23.5618),就会有一个问题.基于科学计数法的浮点计数方法,可以表示很大及很小的数,而不用增加位数,当然也可以表示同时具有整数和小数部分的数.
浮点数(也称为实数)由两部分组成再加上一个符号.尾数(mantissa)是浮点数中用以表示数字数值的部分,大小在 0 和 1 之间.指数(exponent)是浮点数中用以表示小数点(或者二进制小数点)要移动的位数的部分.
十进制数的例子将有助于理解浮点数的基本概念.考虑一个十进制数,以整数形式表示为 241506800.尾数为.2415068,而指数是 9.当把这个整数表示为浮点数时,通过把小数点移动到数字的最左边而将其标准化,使得位数是一个小数,而指数是 10 的幂.这个浮点数写为 $$ 0.2415068 * 10^9 $$ 对于二进制浮点数来说,其格式由 ANSI/IEEE 标准 754-1985 定义为三种形式: 单精度,双精度及扩展精度.除了位数不同之外,它们都具有相同的基本格式.单精度浮点数具有 32 位,双精度浮点数具有64位,而扩展浮点数具有80位.我们的讨论将限于单精度浮点数格式.
单精度浮点二进制数 在单精度浮点二进制数的标准格式中,符号位(S)是最左边的位,指数(E)包括了接下来的 8 位,尾数或者小数部分(F)包括了剩余的 23 位,如下所示:

在尾数或者小数部分,一般认为二进制小数点位于 23 位的左边.为了有效起见,使尾数部分具有 24 位,因为在任何一个二进制数中最左边(MSB)总是为 1.所以,认为这个 1 位于最左边,尽管并没有占用实际的位置.
指数中的 8 位表示的是偏移指数,在实际指数上加上 127 就可以得到.偏移指数的目的是允许表示很大或者很小的数,而不需要为指数赋予一个单独的符号位.偏移指数允许的实际指数范围是–126到+128 .
为了说明二进制数怎样以浮点格式表示,使用1011010010001作为一个例子.首先,它可以表示为1加上一个二进制小数,把二进制小数点向左移动12位然后乘以适当的2的幂. $$ 1011010010001 = 1.011010010001 * 2^{12} $$ 假设这是一个正数,符号位(S)是 0.指数 12 表示为偏移指数的形式,将其加上 127(12+127 =139).该偏移指数(E)表示为二进制数 10001011.尾数是二进制数的小数部分(F),即.011010010001.因为在 2 的幂次表达式中,二进制小数点的左边总是为 1,它并不包含在尾数中.完整的浮点数是

接下来,看看怎样计算以浮点格式表示的二进制数.确定浮点数数值的一般方法如下面的公式所示: $$ 数=(-1)(1+F)(2^{E-127}) $$ 为了说明这个公式,考虑下面的浮点二进制数:

符号位是1.偏移指数是 10010001 = 145.应用这个公式,我们得到 $$ 数=(-1)^1(1.10001110001)(2^{145-127}) \\ =(-1)(1.10001110001)(2^{18})=-1100011100010000000 $$ 这个浮点二进制数等于十进制数的 -407688.因为指数可以是 -126和 +128 之间的任意数,所以最大和最小的数都可以表示出来.32 位的浮点数可以代替具有 129 位的二进制整数因为指数确定了二进制小数点的位置,所以也可以表示同时包含整数和小数部分的数.
浮点数的这种格式有两个例外: 数 0.0 由全 0 来表示,而无穷大的数由指数全 1 和尾数全 0 来表示.