2.7.1 加法

加法中的两个数就是加数和被加数,结果是和.当两个带符号二进制数相加时,有以下4种情况.

1. 两个数都是正的.
2. 正数的数值大于负数的数值.
3. 负数的数值大于正数的数值.
4. 两个数都是负的.

这里使用 8 位带符号数,每次给出一种情况作为例子,也给出相应的十进制数作为对照

◇ 两个正数相加产生一个正数.

两个数都是正的:

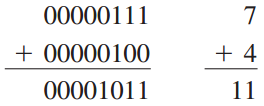
和是正的,因而是二进制原码(非补码).

◇ 正数和负数相加产生一个正数.

正数的数值大于负数的数值:

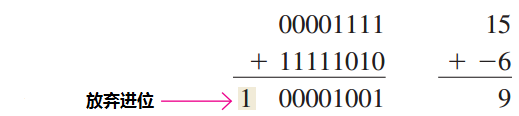
最后的进位被舍去.和是正的,因而是二进制原码(非补码).

◇ 一个正数加上一个较大的负数或者两个负数相加时,生成一个补码形式的负数.

负数的数值大于正数的数值:

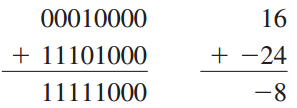
和是负的,所以是补码形式.

两个数都是负的:

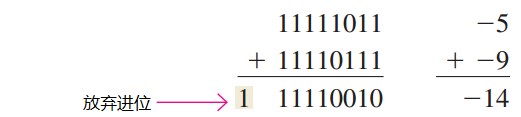
最后的进位被舍去.和是负的,所以是补码形式.

在计算机中,负数是以补码形式保存的,所以正如所见,加法过程是很简单: 将两个数加起来,并舍去最后的任何进位.

溢出条件 当两个数加在一起,而表示和所需的位数超出了这两个数的位数,这时就会发生溢出,并由一个错误符号位指明.溢出仅发生在两个都是正数或者两个都是负数的情况下.如果相加结果得到的符号位和相加的两个数的符号不同,就表明发生了溢出.下面的 8 位数例子将说明这种情况.

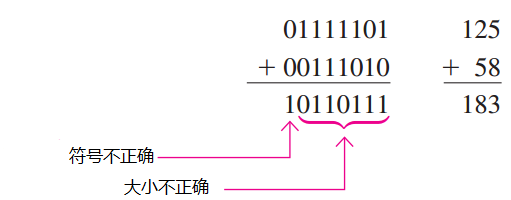
在这个例子中,和 183 需要 8 个数值位.由于数中只有 7 个数值位(有一位是符号位),这时进位就会进人符号位,从而产生溢出指示.

一次加两个数 现在让我们看看数字串相加的情况,即一次加两个数.可以这样操作,首先将前两个数相加,然后两数之和加第三个数,然后再在此和的基础上加第四个数,以此类推.这就是计算机中数字串的相加方法.一次加两个数的方法如例2.19所示.

2.7.2 减法

　◇ 减法是将减数符号改变后的加法.

减法是加法的一个特例.例如,从　＋9(被减数)中减去　＋6(减数)就相当于　+9　加上　-6.基本上,减法运算是改变减数的符号然后加上被减数的运算.减法的结果称为差.

正二进制数或者负二进制数的符号通过求此数的补码而改变.

例如,求取正数　00000100 (+4)的补码时,就会得到　11111100,这就是　–4,权和的计算如下: $$ -128~+64~+32~+16~+8~+4=-4 $$ 作为另一个例子,当取负数 11101101 (-19)的补码时,就会得到 00010011,这就是＋19,权和的计算如下: $$ 16~+2~+1~=~19 $$

◇ 当用补码的方法进行二进制减法时,重要的是两个数要有相同的位数.

由于减法仅仅是减数符号改变后的加法,所以该过程有如下的表述方式:

要将两个带符号数相减,取减数的补码然后相加即可.舍去最后的任何进位.

2.7.3 乘法

乘法中的数分别是被乘数,乘数及积.下面的十进制乘法运算说明了这些数:

在大多数计算机中,乘法运算是通过加法来完成的.正如所见,减法是由加法器完成的,现在看看乘法运算是如何完成的.

◇ 乘法相当于一个数加上它本身,相加的次数就是乘数.

直接加法和部分积是使用加法完成乘法的两种基本方法.在直接加法的方法中,被乘数自身相加的次数等于乘数.在前面的十进制例子(3×8)中,三个被乘数相加: 8+8+8= 24.这种方法的缺点是,如果乘数很大,则运算会变得很冗长.例如,要运算 350×75,必须把 350 自身相加 75 次.顺便说一下,这就是为什么相乘的次数常用来指乘数.

两个二进制数相乘时,这两个数都必须是原码(非补码)的形式.直接加法的方法如例 2.21 所示,每次进行两个二进制数的相加.

部分积方法可能是最常用的一种方法,因为它反映了普通的手工乘法运算.从乘数的最低有效位开始,将被乘数乘以乘数的每一个位.被乘数乘以乘数每一位的结果称为部分积.每一个相继的部分积都向左移动(平移)一位,当产生所有的部分积时,把它们加起来就得到最后的积.这里有一个十进制例子.

乘法运算的积的符号取决于被乘数和乘数的符号,依据下面两条规则:

• 如果符号相同,积就是正值;
• 如果符号不同,积就是负值.

二进制乘法的部分积方法的基本步骤如下所示.

步骤 1: 确定被乘数和乘数的符号是相同的还是相异的,这将决定积的符号.

步骤 2: 把所有的负数变为原码(非补码)形式.因为大多数计算机郁以个吗形八休仔贝双,将负数变换为原码,需要进行补码运算.

步骤 3: 开始于最低有效乘数位,生成部分积.当乘数的位是 1 时,部分积与被乘数就是一样的.当乘数的位是 0 时,部分积就是 0.将每一个相继的部分积向左移动一位.

步骤 4: 将相继的部分积与其前面部分积的和相加,从而得到最终的积.

步骤 5: 如果步骤 1 所确定的符号位是负的,就对积取补码.如果是正的,积就保持为原码.

2.7.4 除法

除法中的数分别是被除数,除数及商.下面给出了标准的除法格式. $$ \frac{被除数}{除数}=商 $$ 计算机中的除法运算是通过减法完成的.由于减法是由加法器完成的,所以除法也可以通过加法器来完成.

除法的结果称为商; 商是除数可以进入被除数的次数.这就是被除数中可以减去多少次除数的次数等于商,如下面的 21 除以 7 所示.

在这个简单的例子中,在余数为0之前除数从被除数中减去了三次,所以商是3.

商的符号取决于被除数和除数的符号,依据以下两条规则:

• 如果符号相同,商就是正的.
• 如果符号不同, 商就是负的.

当两个二进制数相除时,这两个数都必须是原码(非补码)形式.除法的基本过程如下.

步骤1: 确定被除数和除数的符号是相同还是不同,这将确定商的符号.商的初始值是0. 步骤2: 使用补码加法把除数从被除数中减去,得到第一个部分余数,同时将商加 1.如果这个部分余数是正的,转到步骤3: 如果部分余数是 0 或者是负的,就完成了除法. 步骤3: 从部分余数中减去除数,商加上1.如果结果是正的,重复以上步骤得到下一个部分余数.如果结果是零或负的,完成除法.

继续从被除数和部分余数中减去除数,直至出现0或者负数结果.计算除数被减的次数,就会得到商.例2.23使用 8 位带符号二进制数给出了这些步骤.