◇ 十六进制数字系统由数字
0~9和字母A~F组成.
十六讲制数字系统的基是 16,也就是它由 16 个数字和字母共同组成.大多数的数字系统都能成组处理二进制数,即多个4位的组合,这样使用十六进制非常方便,因为每一个十六进制数位就代表了一个 4 位二进制数(如表2.3所示).
10 个数字和 6 个字母字符构成了十六进制数字系统.使用字母 A,B,C, D,E,F 表示数字,初看起来很奇怪,但是请记住任何一种数字系统都是有序符号的集合而已.如果已经理解这些符号表示哪些数,一旦习惯了它们的使用方式,这些符号本身就不重要了.我们将使用下标 16 来指明十六进制数以避免和十进制数相混淆.有时可能会看到十六进制数后面跟随一个"h “.
$$ 表2.3 $$
| 10进制数 | 2进制数 | 16进制数 |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
2.8.1 十六进制计数
计数到F时,怎样在十六进制中计数呢?只要到左侧一列继续计数就可以了,如下所示:
$$ …,~E,~F,~10,~11,~12,~13,~14,~15,~16,~17,~18,~19,~1A,~1B, ~1C,~1D,~1E, \\ ~1F,~20,~21,~22,~23,~24,~25,~26,~27,~28,~29,~2A,~2B,~2C,~2D,~2E,~2F,~30,~31,… $$
利用两个十六进制数位,可以数到 $FF_{16}$,也就是十进制数中的 255.当大于 255 时就需要三个十六进制数位.例如, 100,在十进制数中就是 256, $101_{16}$,在十进制数中就是 257,以此类推.最大的 3 位十六进制数是 $FFF_{16}$,表示十进制数 4095.最大的4位十六进制数是 $FFFF_{16}$,也就是十进制数 65535.
2.8.2 二进制数到十六进制数的转换
把二进制数转换为十六进制数是非常直接的过程.从最右边一位开始,将二进制数每 4 位分成一组,用对等的十六进制符号替代相应的每个 4 位的组合.
2.8.3 十六进制数到二进制数的转换
- ◇ 使用十六进制数来表示二进制数是一个很方便的方法.
把十六进制数转换为二进制数的过程和上述过程相反,使用对等的 4 位的组合替代每个十六进制符号.
- ◇ 十六进制数和二进制数之间的转换直接且容易.
应该清楚,处理十六进制数要比处理相应的二进制数容易一些.因为它们之间的转换很容易,所以十六进制系统在程序设计,打印输出及显示中得到了广泛的应用.
2.8.4 十六进制数到十进制数的转换
一种求十六进制数相应的十进制数的方法是,首先把十六进制数转换为二进制数然后再把二进制数转换为十进制数.
- ◇ 一台计数器可以用来完成十六进制的算术运算.
另一种把十六进制数转换为十进制数的方法是,把每一个十六进制数位的十进制值都乘以该位的权,然后再把这些积加起来.十六进制数的权是 16 的递增幂(从右到左).对于4位十六进制数,它的权是
| $16^3$ | $16^2$ | $16^1$ | $16^0$ |
|---|---|---|---|
| 4096 | 256 | 16 | 1 |
2.8.5 十进制数到十六进制数的转换
用 16 重复除十进制数,就会生成相应的十六进制数,它由相除的余数构成.生成的第一个余数是最低有效数( LSD).以 16 作为除数的每一次相除都会生成一个余数,这个余数就是相应十六进制数的一个数位.这个过程和 2.3 节提到的十进制到二进制转换中重复除以 2 的方法相似.例2.28展示了这个过程.注意当商有小数部分时,用除数乘小数部分就会得到余数.
2.8.6 十六进制加法
可以直接使用 十六 进制数进行加法运算,记住十六进制数 0~9 等同于十进制数 0~9,而十六进制数 A~F 等同于十进制数 10~15.当两个十六进制数相加时,使用下面的方法.(十进制数由下标10表示.)
- 在加法问题任一给定的列中,把两个十六进制数看成它们的十进制值.例如,$5_{16} = 5_{10}$ 和 $C_{16} = 12_{16}$.
- 如果这两个数字的和是 $15_{10}$.或者小些,记下相应的十六进制数.
- 如果这两个数字的和大于 $15_{10}$,记下超出 $16_{10}$ 的量,并在下一列进 1.
2.8.7 十六进制减法
如同前面介绍的,补码允许利用二进制数相加来进行减法的运算.由于十六进制数可以表示二进制数,所以也可以表示二进制数的补码.
有3种方法可以取得十六进制数的补码,方法1最常见也最容易使用,方法2和方法3是替代方法.
方法1 将十六进制数转换为二进制数.取二进制数的补码,把结果转换为十六进制数,如图2.3所示.
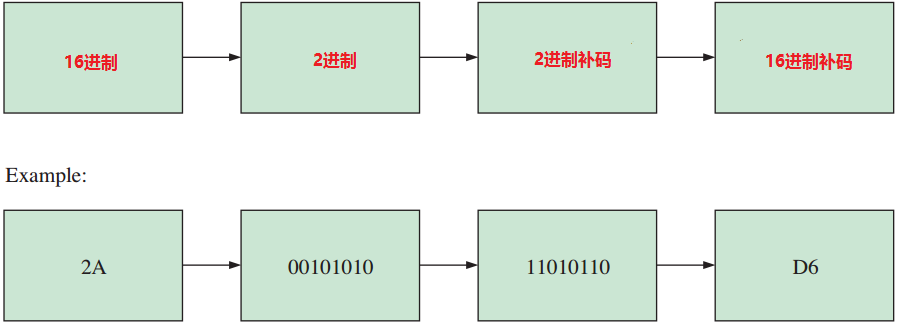
$$ 图2.3 ~~得到十六进制数的补码的方法1 $$
方法2 从最大十六进制数减去当前十六进制数,并加1,如图2.4所示.
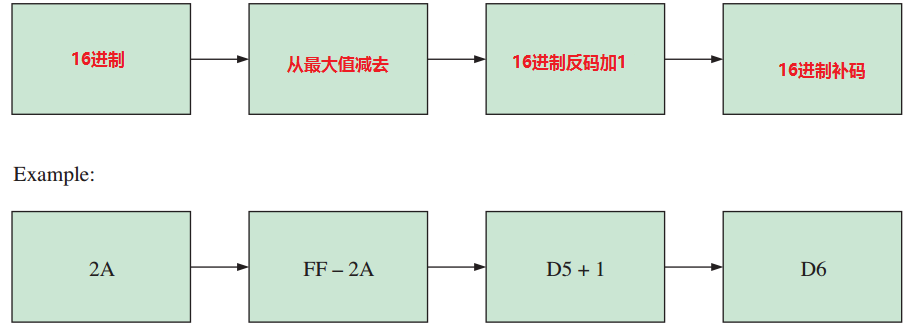
$$ 图2.4~~~ 得到十六进制数的补码的方法2 $$
方法3 写出单个十六进制数的序列.在这一行的下面,以相反的顺序写出这个序列.每个十六进制数的反码就是该数字正下方的数字,结果数加1得到补码,如图2.5所示.
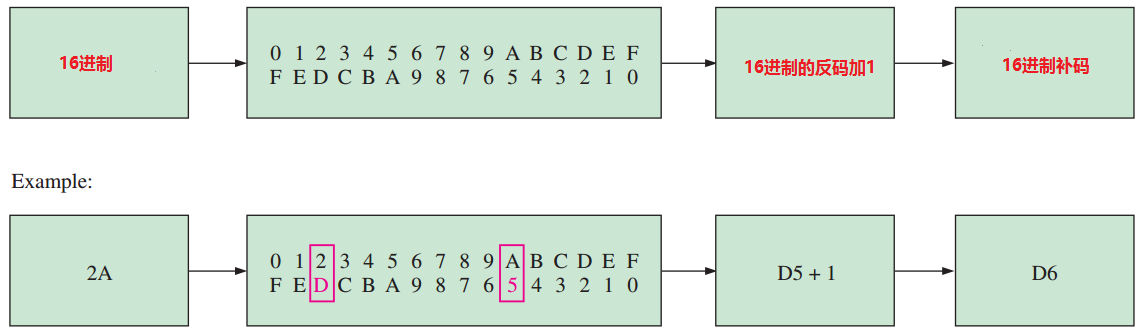 $$
图2.5~~~得到十六进制数的补码的方法3
$$
$$
图2.5~~~得到十六进制数的补码的方法3
$$