八进制数字系统由8个数位组成,它们是

$$ 0，~1,~2，~3,~4，~5,~6，~7 $$

要计大于 7 的数，则从另一列重新开始:

$$ 10,~11 ，~12，~13，~14，~15~，16，~17，~20，~21 ,… $$

• 八进制数字系统的基是 8。

八进制计数和十进制计数比较相似，不同的是没有使用数字 8 和 9。为了区别八进制数和十进制数或者十六进制数，我们使用下标 8 来表示八进制数。例如，八进制 $15_8$ 等于十进制数 $13_{10}$ 和十六进制数D。有时会看到八进制数后面跟随“o”或者“Q”。

2.9.1 八进制数到十进制数的转换

由于八进制数的基是 8,因此每一个相继的数位都是 8 的递增幂，从最右边 $8^0$ 开始, 计算八进制数的相应十进制数的数值，可以通过把每一个数字都乘以其相应的权，并把所得到的积加起来。下面展示了 $2374_8$ 的转换过程。

2.9.2 十进制数到八进制数的转换

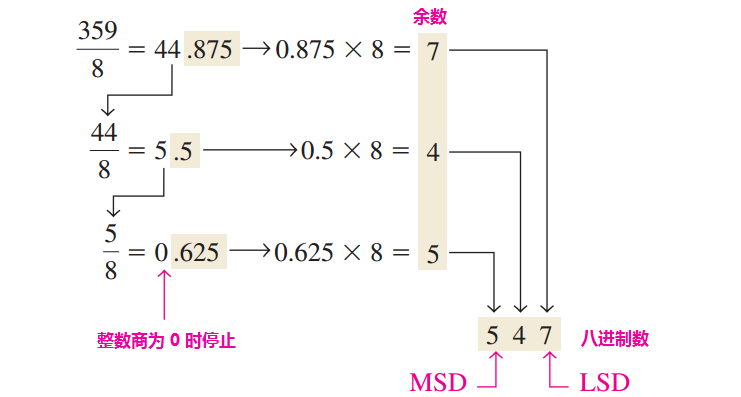
把十进制数转换为八进制数的方法，即重复除以 8 的方法，这和十进制数到二进制数或十六进制数的转换方法相似。为了给出这个过程，我们把十进制数 359 转换为八进制数，以 8 为除数的每一次相继相除都会产生一个余数，而这个余数就会成为相应八进制数的数位。所产生的第一个余数是最低有效数(LSD)。

2.9.3 八进制数到二进制数的转换

• ◇ 八进制是表示二进制数的简洁方法，但是并没有十六进制数常用。

因为每一个八进制数位都可以由一个 3 位二进制数来表示，所以八进制数转换为二进制数很容易。每一个八进制数位由 3 位二进制数表示，如表2.4所示。 $$ 表2.4 ~~~8进制/2进制转换 $$

为了把八进制数转换为二进制数，只要用相应的 3 位二进制数替换每个八进制数位就可以了。这个过程如例2.31所示。

2.9.4 二进制数到八进制数的转换

二进制数到八进制数的转换是八进制数到二进制数的转换的逆过程。如下所述从最右边的 3 位数一组开始，从右向左移动，把每 3 位数一组变换为相应的八进制数。如果最左边的一组没有可用的 3 位数，就加上一个或者两个 0 以形成 3 位一组。前面的 0 不影响二进制数的值。