如前所述，带通滤波器让下限频率和上限频率之间的频率通过，拒绝所有位于通带范围外的频率通过。带通响应可以看作低频响应曲线和高频响应曲线的重叠部分。
学完本节后，你应该掌握以下内容:
- 理解有源带通滤波器
- 描述由低通和高通滤波器构成的带通滤波器
- 确定级联带通滤波器的截止频率和中心频率
- 确定多重反馈带通滤波器的中心频率、带宽和增益
- 解释状态可变带通滤波器的工作原理
9.5.1 低通和高通滤波器的级联形成带通响应
实现带通滤波器的一种方法是将一个高通滤波器和一个低通滤波器级联，如图9-17a所示，只要截止频率分得足够开。每个滤波器都是二极点 Sallen-Key 巴特沃斯结构，下降率为一40dB/十倍频程，如图9-17b中的复合响应曲线所示。如图9-17b所示，每个滤波器截止频率的选择使得响应曲线充分重叠，而且，高通滤波器的截止频率必须比低通滤波器的截止频率足够低。
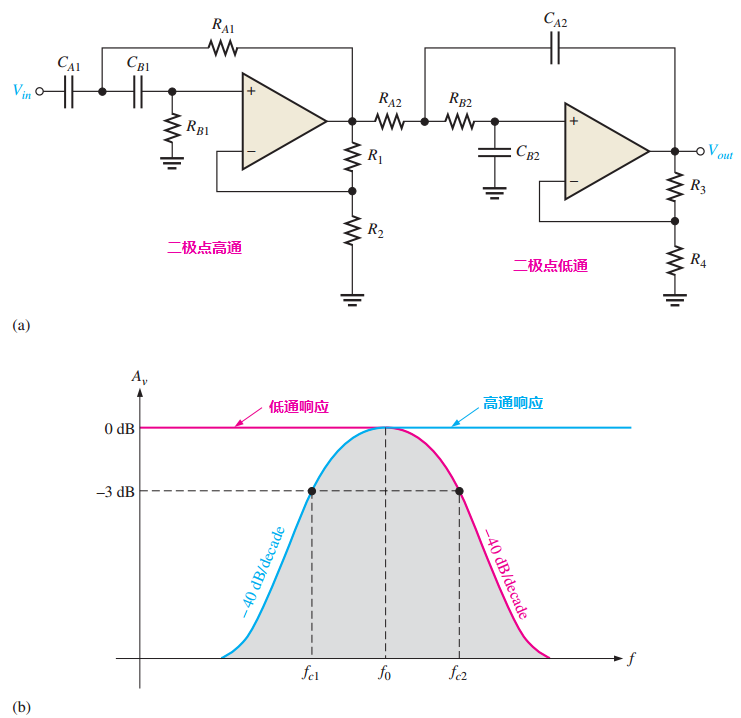$$
图9-17~~~通过二极点高通滤波器和二极点低通滤波器级联形成的带通滤波器
\\
(与两个级联滤波器的级联次序无关)
$$
带通滤波器的下限频率 $f_{c1}$ 是高通滤波器的截止频率，上限频率是低通滤波器的截止频率 $f_{c2}$ 。理想情况下，如前所述，通带的中心频率 $f_0$ 是 $f_{c1}$ 和 $f_{c2}$ 的几何平均值。下面的公式给出了图9-17中带通滤波器三个频率之间的关系。 $$ f_{c1}=\frac{1}{2\pi \sqrt[]{R_{A1}R_{B1}C_{A1}C_{B1}}} \\ f_{c1}=\frac{1}{2\pi \sqrt[]{R_{A2}R_{B2}C_{A2}C_{B2}}} \\ f_0=\sqrt[]{f_{c1}f_{c2}} $$
当然，如果在实现每个滤波器时使用等值元件，截止频率的公式可以简化为 $f_c = 1/2\pi RC$.
9.5.2 多重反馈带通滤波器
另一种类型的滤波器结构是多重反馈带通滤波器，如图9-18所示。通过 $R_2$ 和 $C_1$ 有两条反馈路径，元件 $R_1$ 和 $C_1$ 提供低通响应，$R_2$ 和 $C_2$ 提供高通响应。最大增益 $A_0$ 在中心频率处产生。Q 值小于 10 的滤波器属于这种类型。从 $C_1$ 反馈路径看，$R_1$和 $R_3$ 并联(将$V_{in}$源用短路替代)，中心频率的表达式可以表示为:
$$
f_0=\frac{1}{2\pi \sqrt[]{(R_1||R_3)R_2C_1C_2}}
$$
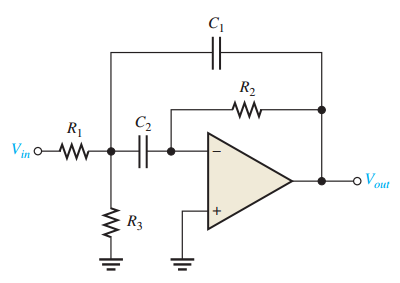$$
图9-18~~~多重反馈带通滤波器
$$
令 $C_1=C_2=C$，得到(推导见附录): $$ f_0=\frac{1}{2\pi C}\sqrt[]{\frac{R_1+R_3}{R_1R_2R_3}}~~~(9-7) $$
给电容器选择一个方便的值以便于计算，然后根据期望的 $f_0、BW$ 和 $A_0$ 来计算三个电阻的值。你知道，Q 值可以通过 $Q=f_0/BW$ 计算，电阻可以通过如下公式计算得到(没有给出具体的推导过程)。 $$ R_1=\frac{Q}{2\pi f_0CA_0} \\ R_2=\frac{Q}{\pi f_0C} \\ R_3=\frac{Q}{2\pi f_0C(2Q^2-A_0)} $$
为了得到增益表达式，从前面两个公式中推出Q。 $$ Q=2\pi f_0A_0CR_1 \\ Q=\pi f_0CR_2 $$ 于是, $$ 2\pi f_0A_0CR_1=\pi f_0CR_2 $$ 中心频率处的最大增益为 $$ A_0=\frac{R_2}{2R_1}~~~(9-8) $$
为了让公式 $R_3=Q/[2\pi f_0C(2Q^2-A_0)]$ 的分母为正, $A_0<2Q^2$, 这使得增益受到限制.
9.5.3 状态可变带通滤波器
状态可变或通用有源滤波器广泛用于带通应用。如图9-20所示，它由一个求和放大器和两个运放积分器(作为单极点低通滤波器)通过级联方式构成的二阶滤波器。尽管状态可变结构主要用作带通(BP)滤波器，但它也可用作低通(LP)和高通(HP)输出，中心频率由两个积分器中的 RC 网络决定。当用作带通滤波器时，通常把积分器的截止频率设置为相等，这样就设置了通带的中心频率。
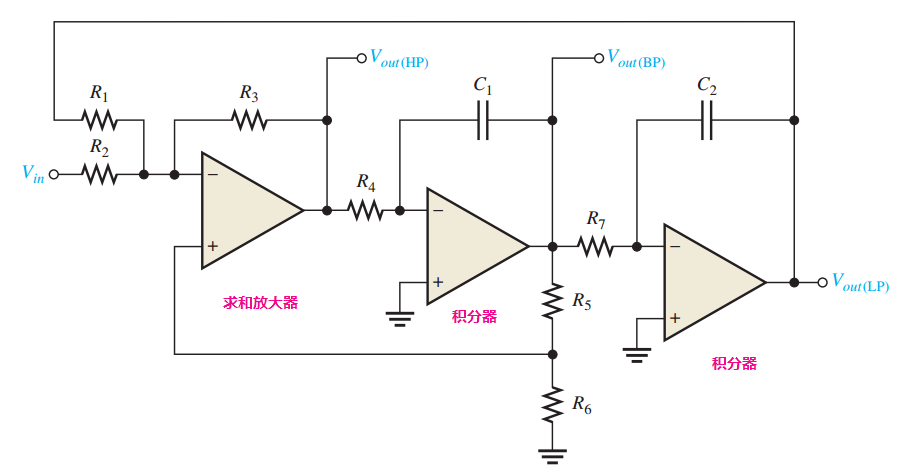$$
图9-20~~~状态可变的带通滤波器
$$
基本工作原理 当输入端频率低于 $f_c$ 时，输入信号通过求和放大器和积分器，并反馈180°的相位。因此，对所有低于 $f_c$ 的频率，反馈信号和输入信号相互抵消。随着积分器的低通响应下降，反馈信号减小，因此允许输入信号通过带通输出。当频率高于 $f_c$ 时，低通响应逐渐消失，因此阻止输入信号通过积分器。所以，带通输出在 $f_c$ 达到峰值，如图9-21所示。这种类型的滤波器可以得到直至 100 的稳定 Q 值。Q 值由反馈电阻 $R_5$ 和 $R_6$ 决定，公式如下。
$$
Q=\frac{1}{3}(\frac{R_5}{R_6}+1)
$$
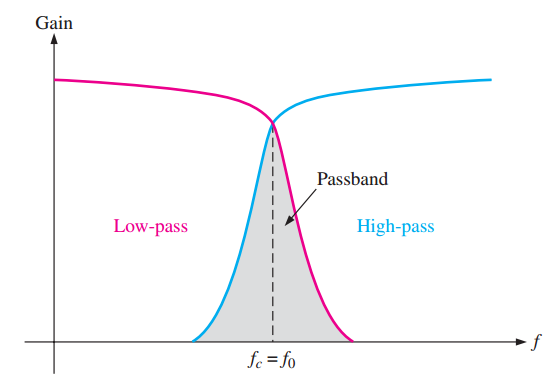$$
图9-21~~~状态可变滤波器的通用响应曲线
$$
状态可变滤波器不能同时优化低通、高通和带通性能，这是因为: 为了优化低通或高通巴特沃斯响应，DF 必须等于 1.414。因为 Q=1/DF，所以 Q 为 0.707。这样低的 Q 值提供的带通响应非常差(大的 BW 和较差的选择性)。若当作带通滤波器来优化，Q 值必须设置成很大。