Back

11.2 PD控制器的设计

前面讨论的所有控制系统中的控制器都是常数增益为K的放大器，控制器输出的控制信号只与控制器的输人呈简单的系数比例关系，这类控制方式称为比例控制。

从直观上讲，除了比例运算外，我们也应该能够使用输入信号的微分或积分运算,因此，更为一般的连续控制器应包括加法器(加法或减法)、放大器、衰减器、微分器和积分器等元件。设计者的任务就是要确定采用其中的哪些元件，用多大的比例，以及如何把它们连接在一起。例如，在实际应用中最常用的一类控制器就是 PID 控制器，三个字母分别表示比例(Proportional)、积分(Integral)、微分(Derivative)，在 PID 控制器中微分和积分部分都有各自的性能含义。要想应用这些部分，就必须理解它们的基本特性。为此,首先我们考虑 PD 控制。

任意一个二阶反馈控制系统的控制框图如 图11-3 所示，其传递函数为 $$ G_p(s) = \frac{ω^2_n}{s(s+2ξω_n)}~~~~(11-1) $$

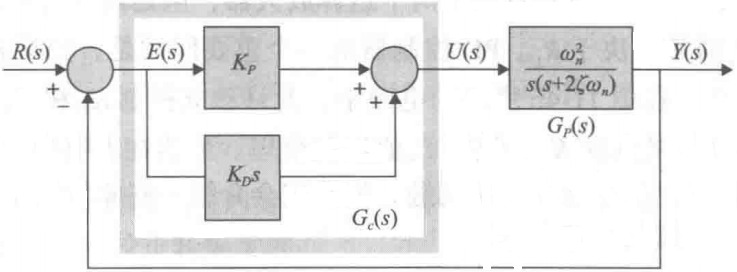Automatic图11-3.png $$ 图11-3~~~具有PD控制器的控制系统控制框图 $$

采用比例-微分(PD)控制的串联控制器的传递函数为 $$ G_c(s) = K_p+K_DS~~~(11-2) $$ 因此,系统的控制信号为 $$ u(t) = K_pe(t)+K_D\frac{de(t)}{dt}~~~(11-3) $$

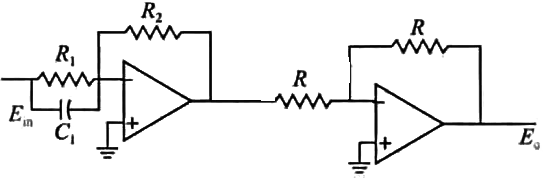
式中，$K_p$ 和 $K_D$ 分别是比例和微分系数。用表6-1中的元件，我们可以得到 PD 控制器的两种电路实现，如图11-4所示。图11-4a所示电路的传递函数为 $$ \frac{E_o(s)}{E_{in}(s)} = \frac{R_2}{R_1}+R_2C_1s~~~(11-4) $$ 比较式（11-2）和式（11-4）可得到: $$ K_p = R_2/R_1~~~~ K_D = R_2C_1~~~(11-5) $$ 图11-4b所示电路的传递函数为 $$ \frac{E_o(s)}{E_{in(s)}} = \frac{R_2}{R_1}+R_dC_ds~~~(11-6) $$ 同样,由式（11-2）和式(11-6)得到: $$ K_p = R_2/R_1~~~~~K_D = R_dC_d~~~~(11-7) $$

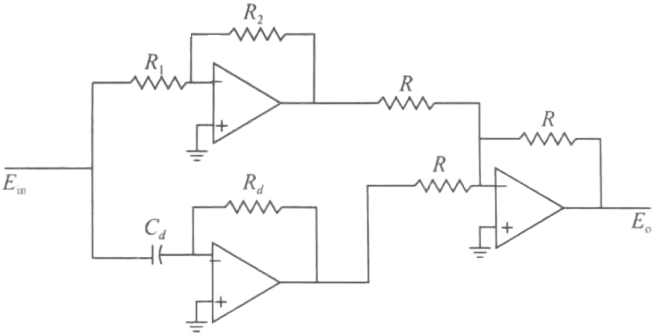Automatic图11-4a.png Automatic图11-4b.png $$ 图11-4 ~~~PD控制器的运算放大器电路实现 $$

图11-4a 所示电路的优点是只用了两个运算放大器，但是该电路不允许独立选择 $K_P$ 和$K_D$, 因为它们通常取决于 $R_2$。PD 控制器的一个重要问题是，如果 $K_D$ 的值很大，则需要大的电容器 $C_1$。在 图11-4b 所示的电路中，允许独立控制 $K_P$ 和 $K_D$ 值。可以选择一个较大的 $R_d$ 值来补偿较大的 $K_D$,使得$C_d$，值比较合理。虽然在本书中我们不可能顾及设计控制器传递函数中的所有实际应用问题，但我们会介绍一些非常重要的注意事项。

校正系统前向通道的传递函数为 $$ G(s) = \frac{Y(s)}{E(s)}=G_c(s)G_p(s)=\frac{ω^2_n(K_p+K_Ds)}{s(s+2ξω_n)}~~~(11-8) $$ 这表明 PD 控制相当于给系统前向通道传递函数在 $s =-K_p/K_D$ 处增加了一个单零点。

11.2.1 PD控制的时域分析

PD 控制系统的瞬态时间响应曲线如 图11-5 所示，图11-5a 给出了具有比例控制的稳定系统单位阶跃响应曲线，从图中可以看到只具有比例控制的系统阶跃响应曲线具有偏大的最大超调量，并且振荡也很大。图11-5b 和 c 分别表示误差信号(即单位阶跃输入和输出 $y(t)$ 之差)及其对时间的导数 $de(t)/dt$。从 $e(t)$ 和 $de(t)/dt$ 这两个值的变化也可以看出系统的超调特性和振荡特性。为了方便解释，我们假设系统包含一个其转矩与 $e(t)$ 成正比的电动机。比例控制系统的性能分析如下:

  1. 在时间段 0<t<$t_1$内: 误差信号 $e(t)$ 为正，电动机转矩也为正并且迅速增加。此时,转矩过大使得输出 $y(t)$ 产生大的超调和振荡，在这个时间段中无阻尼。
  2. 在 $t_1$<t<$t_3$内: e(t)为负，相应的转矩也为负。负转矩阻碍了输出的增长，最终使得输出 $y(t)$ 反向，低于额定值。
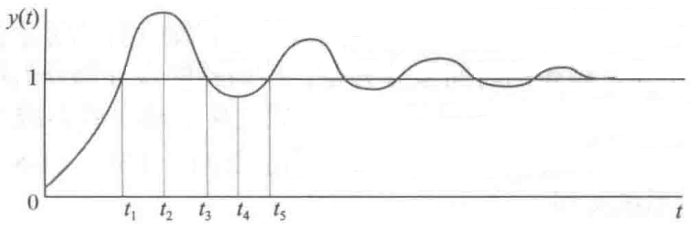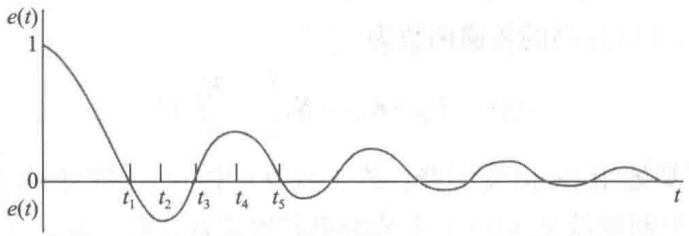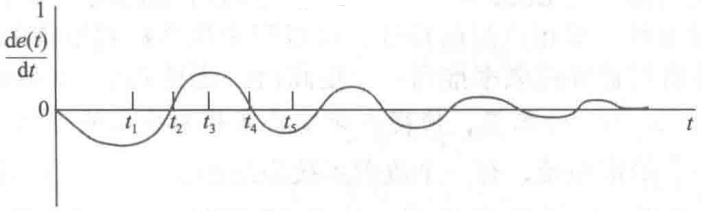  3. 在 $t_3$<t<$t_5$内: 转矩再次为正，这样弥补了在上一个时间段由负转矩产生的欠调。由于假定系统是稳定的，所以每次振荡都会减小误差幅度，并且输出最终会达到稳定值。 Automatic图11-5a.png $$ a)单位阶跃响应y(t)曲线 $$ Automatic图11-5b.png $$ b)误差e(t)曲线 $$ Automatic图11-5c.png $$ c)误差信号随时间变化的de(t)/dt曲线 $$ $$ 图11-5 微分控制下的y(t)、e(t)和 de(t)/dt的波形图 $$

考虑到以上对系统时间响应的分析，可以得出造成高超调的因素主要有

  1. 在 0<t<$t_1$, 正向校正转矩太大。
  2. 在 $t_1$<t<$t_2$, 制动转矩不合适。

因此，为了减小阶跃响应中的超调而又不明显增加上升时间的一种合理方法是:

  1. 当 0<t<$t_1$时，减小正向校正转矩的幅值。
  2. 当 $t_1$<t<$t_2$时,增大制动转矩。

同理，在时间段 $t_2$<t<$t_4$ 内，应该减小在 $t_2$<t<$t_3$ 中的负向校正转矩，增加 $t_3$<t<$t_4$ 时间段内正向的制动转矩,由此来改善 $y(t)$ 的欠调。

由式（11-2）描述的 PD 控制精确给出所需的补偿效果，式（11-3）给出PD控制的控制信号，从图11-5c可看出 PD 控制器具有如下作用:

  1. 当 0<t<$t_1$, $de(t)/dt$ 为负，抑制了由 $e(t)$ 单独作用产生的原始转矩的增加。
  2. 当 $t_1$<t<$t_2$, $e(t)$ 和 $de(t)/dt$ 都为负，这意味着产生的负向制动转矩将大于只采用比例控制时的负向制动转矩。
  3. 当 $t_2$<t<$t_3$, $e(t)$ 和 $de(t)/dt$ 都反向,减小了产生欠调的负向制动转矩。

上述这些作用会使 $y(t)$ 产生较小的超调和欠调。

我们还可以从另外一种角度来看待 PD 控制。由于 $de(t)/dt$ 表示 $e(t)$ 的斜率，PD 控制在本质上是一种超前控制,即知道了斜率，控制器可以预料到误差的方向由此来更好地控制系统。通常情况下，在线性系统中，如果由阶跃响应得到的 $e(t)$ 或 $y(t)$ 的斜率很大，相应地就会产生较大的超调量，微分控制测得 $e(t)$ 的瞬间斜率，提前预测出大的超调量,在大超调产生之前做出适当的校正。

直观上讲，微分控制只有当系统的稳态误差随时间发生变化时才会起作用。如果稳态误差随时间保持不变，误差的时间微分为零，控制器的微分部分就不能给系统提供输入。当稳态误差随时间增加时，转矩与 $de(t)/dt$ 成比例变化，就会减小误差幅值。我们知道控制系统的类型影响单位反馈控制系统的稳态误差，由式（11-8）可以清楚地看到 PD 控制并没有改变系统类型。

11.2.2 PD控制的频域分析

在频域设计中, PD 控制的传递函数为 $$ G_{c(s)} = K_p+K_DS = K_p(1+\frac{K_D}{K_P}S)~~~(11-9) $$ 这样可以更容易地用 Bode 图解释。式(11-9)中 $K_p=1$ 的 Bode 图如图11-6所示。一般情况下，比例控制增益 $K_p$ 可以和系统的串联增益合并在一起，这样PD控制器的零频增益可看成单位增益。由Bode图11-6可以看出 PD 控制器是一个高通滤波器，有高通滤波器的高通滤波性，即相位超前特性，可以用来提高控制系统的相位裕量。但PD控制器的幅值特性将增益穿越频率推到一个更高值。这样 PD 控制器的设计原理就涉及控制器交接频率 $\omega=K_P/K_D$ 的配置，使得在新增益穿越频率点处可以有效地改善系统的相位裕量。对于一个给定系统，有一个改善系统阻尼的 $K_P/K_D$ 最佳范围。在 PD 控制器的实际设计中，还要考虑选择 $K_P$ 和 $K_D$ 值。由于 PD 控制器的高通特性，在频域中 PD 控制器的另一个显著优点是，在大部分情况下增加了控制系统的 BW，同时减小了阶跃响应的上升时间，但它的缺点是高通滤波器的微分部分放大了系统在输入处的高频噪声。

11.2.3 PD控制的作用总结

虽然PD控制器对有轻微振荡或初始不稳定的系统不适用，但正确设计的 PD 控制器可能通过以下几个方面影响控制系统的性能:

  1. 改善阻尼,减小最大超调量。
  2. 缩短上升时间和调节时间。
  3. 增加 BW。
  4. 改善 GM、PM 和 $M_r$.
  5. 可能放大高频噪声。
  6. 在电路实现中可能需要相当大的电容。 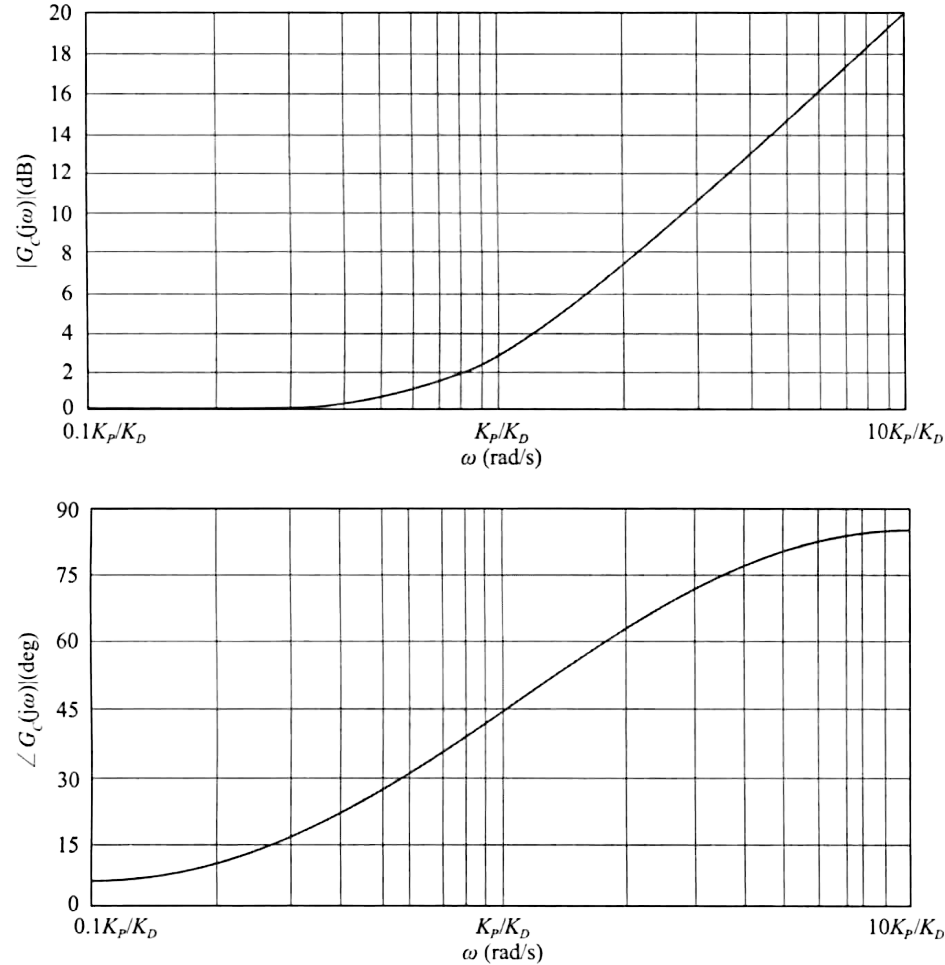Automatic图11-6.png $$ 图11-6~~~1+\frac{K_DS}{K_p},K_p=1的Bode图 $$

下面几个例子解释了 PD 控制器对二阶系统的时域响应和频域响应的影响。