11.5 相位超前和相位滞后控制器的设计

在校正控制系统中， PID 控制器及其组成部分 PD 和PI控制器是对控制系统进行微分、积分操作。一般来说，我们可以把控制系统的控制器设计看作滤波器设计问题，这样就会有很多可能的设计方案。从滤波角度来看， PD 控制器可以看作高通滤波器,PI控制器可以看作低通滤波器，而 PID 控制器根据控制器参数值的不同，可以看成带通滤波器或带阻滤波器。在本节中，我们所介绍的高通滤波器可以称为相位超前控制器，因为它给控制系统引入的正向相位超出了一定的频率范围。低通滤波器因为引入了负向相位，因此称为相位滞后控制器。两种控制器所对应的电路如图11-30所示。 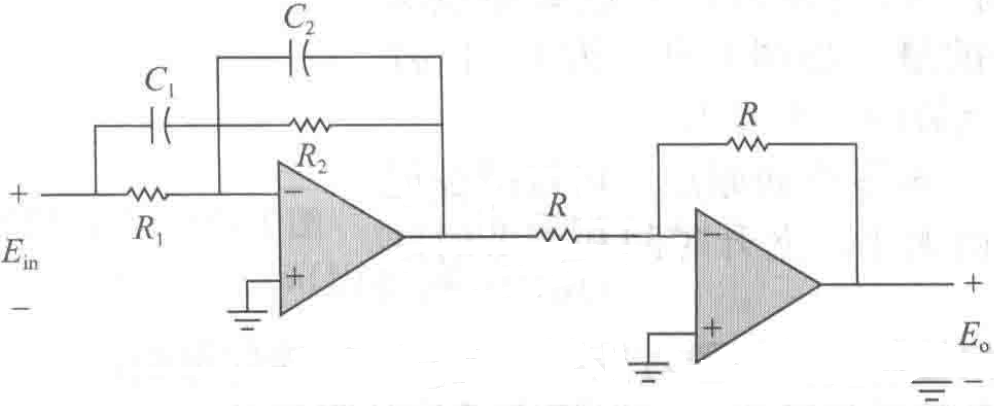Automatic图11-30.png $$ 图11-30\ G_c(s)=K_c\frac{S+Z_1}{S+P_1}的运算放大电路 $$ 一个简单的相位超前或相位滞后控制器的传递函数表达式为 $$ G_c(S) = K_c\frac{S+Z_1}{S+P_1} \ (11-69) $$ 如果 $p_1>z_1$，控制器为高通滤波器或相位超前控制器;如果$p_1>z_1$，控制器为低通滤波器或相位滞后控制器。

式(11-69)所示运算放大电路的实现可见第6章的表6-1g,并在图11-30中使用倒置放大器再次重现。该电路的传递函数可以写为 $$ G_c(S) = \frac{E_o(S)}{E_{in}(S)}=\frac{C_1}{C_2}\frac{S+\frac{1}{R_1C_1}}{S+\frac{1}{R_2C_2}} \ (11-70) $$

对比式( 11-69)和式( 11-70)，可得: $$ K_c = C_1/C_2\ (11-71)Z_1 = 1/R_1C_1\ P_1=1/R_2C_2 $$ 令$C=C_1=C_2$，可以将所需设计的参数从4个减少到3个，则式(11-70)可以写为 $$ G_c(S)=\frac{R_2}{R_1}(\frac{1+R_1C_s}{1+R_2C_s})=\frac{1}{a}(\frac{1+aTs}{1+Ts})\(11-72) $$ 其中： $$ a = \frac{R_1}{R_2}\(11-73) $$ $$ T = R_2C\(11-74) $$

11.5.1相位超前控制器的时域分析和设计

在本节中，我们首先考虑式(11-70)和式(11-72)所表示的相位超前控制器($z_1<p_1$或$a>1$)。为了使得加人相位超前控制器后，系统的稳态误差指标不会下降，式(11-72)中的因子 a 应当包含在前向通道增益系数$K$中。因此可以写为 $$ G_c(s) = \frac{1+aTs}{1+Ts}，a>1\(11-75) $$ 式(11-75)的零极点配置图如图11-31所示。根据第7章中的讨论，在前向通道传递函数中加入一对零极点(零点很接近原点)对控制系统会产生影响，若相位超前控制器的参数选择合理，则可以提高闭环系统的稳定性。超前控制器设计从本质上讲就是合理地配置 $G_c(s)$ 的零点，使得控制系统满足实际要求。根轨迹方法可以用来确定参数范围。以下列出的是选择参数a和T的几点指导性原则:

将零点 $-1/aT$ 移向原点可以改善系统的.上升时间和调节时间。但是如果该零点离原点太近，就会导致系统的最大超调上升，因为 $-1/aT$ 也是闭环系统传递函数的一个零点。
令极点$-1/T$远离零点和原点，可以减少最大超调，但若$T$的值太小，上升时间和调节时间又会增加。

我们总结一下相位超前控制器对控制系统时域特性的影响:

若控制器的参数选择适当，可以提高系统的阻尼性。
可以改善上升时间和调节时间。
根据式(11-75)，相位超前控制器不会影响系统的稳态误差，因为$G_c(0)=1$。

11.5.2相位超前控制器的频域分析和设计

式(11-75)所表示的相位超前控制器的Bode图如图11-32所示。两个交接频率为$∞=1/aT$和 $∞=1/T$。下面将推导出最大的相位值 $\phi_m$ 和对应的频率$\omega_m$。因为$\omega_m$是两个交接频率的几何平均值，所以有: $$ lg \omega_m = \frac{1}{2}(lg\frac{1}{aT}+lg\frac{1}{T})\(11-76) $$ 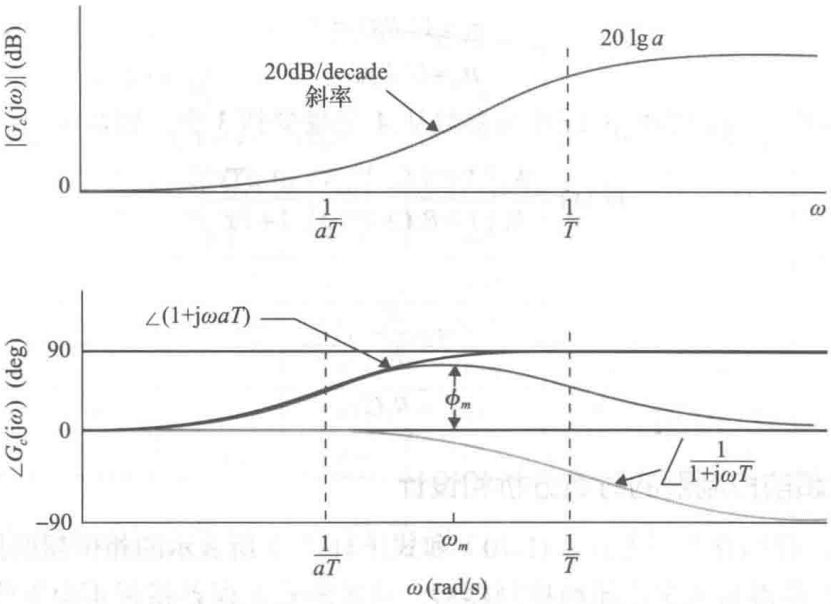Automatic图11-32.png $$ 图11-32相位超前控制器G_c(s)=\frac{1+ aTs}{1+ Ts}，a>1的Bode图 $$ 因此 $$ \omega_m = \frac{1}{\sqrt[]aT}\(11-77) $$ 为了确定最大相位$\phi_m$，$G_c(j\omega)$ 的相位可以写成 $$ ∠G_c(j\omega)=\phi(j\omega)=arc\tan ωaT-arc\tan ωT\(11-78) $$ 由此可得到: $$ \tan \phi(j\omega)=\frac{ωaT-ωT}{1+(ω aT)(ωT)}\(11-79) $$ 将式(11-77)代入式(11-79)可得: $$ \tan\phi_m = \frac{a-1}{2\sqrt[]a}\(11-80) $$ 或 $$ \sin\phi_m = \frac{a-1}{a+1}\(11-81) $$

因此，只要知道 $\phi_m$ 的值，就可以得到 a 的值: $$ a = \frac{1+\sin\phi_m}{1-\sin\phi_m}\(11-82) $$

相位$\phi_m$和a之间的关系以及相位超前控制器Bode图的一-般性质为频域设计提供了一些便利。当然，困难在于确定时域和频域特性之间的相关性。频域中相位超前控制器设计的概要如下，假设设计要求仅涉及稳态误差和相位裕度。

根据稳态误差要求，增益常数K被用于构造 $G_p(j\omega)$ 的Bode图。一旦确定了a的值，就必须向上调整K的值。
确定待校正系统的相位裕度和增益裕度，并确定实现相位裕度所需的相位超前量。根据所需的相位超前量，相应地估计所需的 $\phi_m$ 值，并根据式(11-82)计算a的值。
一旦a的值确定，只需要确定T值，设计大体上就完成了。同时还要配置好相位超前控制器的两个交接频率$1/aT$和$1/T$，这样就将 $\phi_m$ 放置在了新增益穿越频率 $\omega’_g$ 处，可以达到校正系统的相位裕量。已知相位超前控制器的高频增益为20lgadB。因此，为了得到在 $\omega_m$ 处的新增益穿越频率，也就是$1/aT$和$1/T$的几何平均值，我们需要将 $\omega_m$ 放置在待校正系统 $G_P(j\omega)$ 的$-10lga dB$幅值处，来使得幅值曲线增加$10lga dB$，从而使得在 $\omega_m$ 处达到0dB。
检查校正系统前向通道传递丽数的Bode图，看所有的性能指标是否都已满足。如果没有，重新选择$\phi_m$的值，重复上述步骤。
如果设计要求全部满足，则相位超前控制器的传递由 a 和 T 的值确定。

如果设计要求中还包括$M_r$或 BW 等指标，就要用Nichols表或计算机编程来进行

11.5.3 相位超前控制的作用

从上面列举的两个例子，下面总结一-下单阶相位超前控制器的作用和局限性。

相位超前控制器给控制系统的前向通道传递函数增加了–对零极点，其中零点在极点的右边。一般而言，这使得闭环系统的阻尼增大，.上升时间和调节时间减小。
控制系统的前向通道传递函数在增益穿越频率点附近的相位增加，改善了闭环系统的相位裕量。
控制系统前向通道传递函数的幅值曲线斜率在增益穿越频率点处减小。这通常会改善系统增益和相位裕量，从而改善系统的相对稳定性。
闭环系统的带宽增加，对应于时间响应变快。
控制系统的稳态误差没有影响。

11.5.4 单阶相位超前控制的局限性

一般而言，相位超前控制器并不适合所有系统。单阶相位超前控制器要能成功地用于改进系统的稳定性要依赖如"下条件:

带宽的考虑:如果原始系统不稳定或稳定裕量较小，则实现期望的相位裕量所需的相位超前量可能会过多。这会使得控制器的a值很大，结果导致校正系统产生较大的带宽，从而会使在输人端进人系统的高频噪声产生较大的影响。但是，如果噪声是在输出附近进入系统，增加的带宽对抑制噪声是有利的。并且带宽越大，控制系统的鲁棒性越好，也就是说，系统对参数变化不敏感，并如前面所说的可以抑制噪声。
如果原始系统不稳定，或只具有较小的稳定裕量，控制系统前向通道传递函数的相位曲线在增益穿越频率点附近的负斜率很大。在这种情况下，由于在新增益穿越频率点处的附加的相位超前是加在-一个远小于原来的增益穿越频率点处相位值的相角上的，单阶相位超前控制器不再有效，只有采用非常大的a值来实现期望的相位裕量，而a值越大就需要越高的放大器增益K,因此必须增大K值，这样在实际应用中的造价成本就会很大。

如例11-5-2所示，校正系统的欠调可能比超调大。通常，即使满足了所需的相位裕量，一部分相位曲线仍可能会跌落到180°以下，从而形成条件稳定的系统。 3. 单阶相位超前控制器最大允许的相位超前不会超过90%。因此如果需要大于90° 的相位超前，就必须用多阶控制器。

11.5.5 多阶相位超前控制器

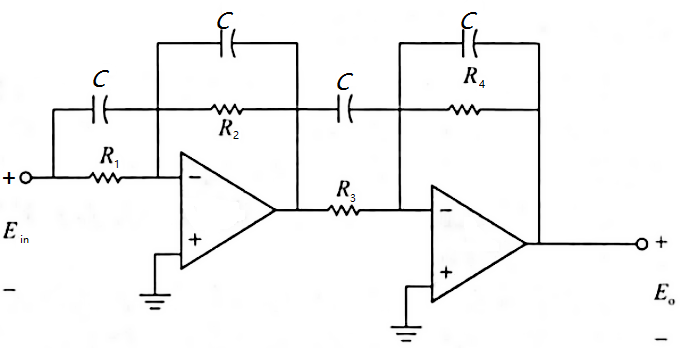Automatic图11-42.png $$ 图11-42 二二阶相位超前(滞后)控制器的电路实现 $$ 当进行相位超前控制器设计需要增加的相位超过90°时，就需要用到多阶相位超前控制器。图11-42给出了一个二阶相位超前控制器的电路实现图，电路图的输人-输出传递函数为 $$ G_c(s) = \frac{E_o(s)}{E_{in}(s)} = (\frac{s+\frac{1}{R_1C}}{s+\frac{1}{R_2C}})(\frac{s+\frac{1}{R_3C}}{s+\frac{1}{R_4C}})=\frac{R_2R_4}{R_1R_3}(\frac{1+R_1C_S}{1+R_2C_S})(\frac{1+R_3C_S}{1+R_4C_S})\(11-119) $$ 或者是 $$ G_c(s) = \frac{1}{a_1a_2}(\frac{1+a_1T_1s}{1+T_1s})(\frac{1+a_2T_2s}{1+T_2s})\(11-120) $$ 其中，$a_1=R_1/R_2，a_2=R_3/R_4， T_1=R_2C，T_2=R_4C$。

由于现在需要配置更多的极点和零点，因此在时域中进行多阶相位超前控制器的设计会变得更加烦琐。因为存在更多的可变参数，所以根轨迹方法的使用也变得难以操作。在这种情况下，频域设计是一种更好的设计选择。例如对于一个二阶控制器，我们可以先选好第一阶的参数值，使得部分相位裕量满足要求，然后再使得第二阶满足剩余的要求。一般来说，这两个阶段的设计是不相同的。下面的例子将详细阐述二阶相位超前控制器的设计过程。

11.5.6 灵敏度考虑

灵敏度函数的定义出现在10.15节中，式( 11-128)可以用来作为衡量控制系统鲁棒性的一个性能指标。闭环传递函数关于前向通道传递函数变化的灵敏度定义为 $$ S^M_G(s) = \frac{\partial{M(s)}/M(s)}{\partial{G(s)}/G(s)}=\frac{G^{-1}(s)}{1+G^{-1}(s)}=\frac{1}{1+G(s)}\(11-128) $$