反相器的标准逻辑符号如图3.1所示,(a)图给出了特殊形状符号,(b)图给出了矩形轮廓符号.在这本书中,一般使用特殊形状符号;但是,矩形轮廓符号常常出现在许多工业出版物中,所以也应该熟悉它们.(逻辑门符号依据 ANSI/IEEE 标准 91-1984.)
3.1.1 否定和极性指示
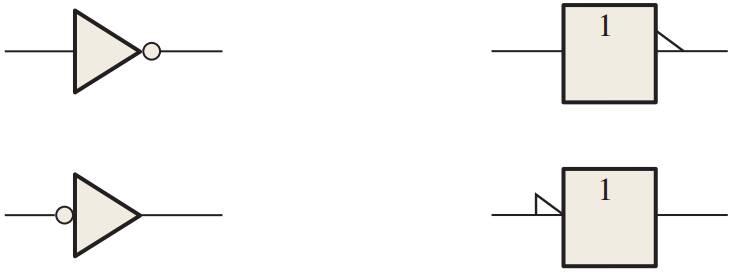 $$
(a)具有否定指示的特殊形状符号~~~~~~~~~~(b)具有极性指示的矩形轮廓符号
$$
否定指示是一个小圆圈(o),当其出现在任何逻辑元件的输入或者输出位置时,为反相或者为反码,如图3.1(a)的反相器所示.一般情况下,输入位于逻辑符号的左侧而输出位于右侧.当出现在输人位置时,小圆圈就表示 0 电平有效或者是确定的输入状态,而这个输入称为低电平有效输人.当出现在输出位置时,该小圆圈就指明0有效或者是确定的输出状态,而这个输出称为低电平有效输出.当输人或者输出没有小圆圈时,就表示1是有效的或者是确定的状态,而这个输入或输出称为高电平有效.
$$
(a)具有否定指示的特殊形状符号~~~~~~~~~~(b)具有极性指示的矩形轮廓符号
$$
否定指示是一个小圆圈(o),当其出现在任何逻辑元件的输入或者输出位置时,为反相或者为反码,如图3.1(a)的反相器所示.一般情况下,输入位于逻辑符号的左侧而输出位于右侧.当出现在输人位置时,小圆圈就表示 0 电平有效或者是确定的输入状态,而这个输入称为低电平有效输人.当出现在输出位置时,该小圆圈就指明0有效或者是确定的输出状态,而这个输出称为低电平有效输出.当输人或者输出没有小圆圈时,就表示1是有效的或者是确定的状态,而这个输入或输出称为高电平有效.
极性或者电平指示是一个"三角形"(◣),当其出现在任何逻辑元件的输人或者输出位置时,表示反相,如图3.1(b)所示.当其出现在输入位置时,就表示低电平是有效的或者是确定的输人状态.当其出现在输出位置时,就表示低电平是有效的或者是确定的输出状态.
两种指示(小圆圈或三角形)都可以用在特殊形状符号和矩形轮廓符号中.图3.1(a)给出的是本书后面主要使用的反相器.注意反相或极性指示的不同放置并不意味着反相器运算方式的改变.
3.1.2 反相器真值表
当反相器的输入是高电平时,它的输出就是低电平。当反相器的输入是低电平时,它的输出就是高电平。这种运算总结于表3.1中,表中以电平和对应的位值给出了每个可能的输入和与之对应的输出。这样的表称为真值表。 $$ 表3.1~~~反相器真值表 $$
| 输入 | 输出 |
|---|---|
| 低(0) | 高(1) |
| 高(1) | 低(0) |
3.1.3 反相器运算
图3.2给出了反相器脉冲输入和相应的输出,其中 $t_1$ 和 $t_2$ 指明了在输人和输出波形上相对应的点。
当输入为低电平时,输出就是高电平; 当输入是高电平时,输出就是低电平,因此产生反相的输出脉冲。
 $$
图3.2~~~具有脉冲输入的反相运算。打开文件FO3-02检验反相操作
$$
$$
图3.2~~~具有脉冲输入的反相运算。打开文件FO3-02检验反相操作
$$
3.1.4 时序图
- ◇ 时序图给出了两个或者更多的波形在时间上的相互关系。
回顾第1章我们知道,基本上时序图是基于时间的、准确显示两个或者更多波形相互之间关系的图形。例如,图3.2中输出脉冲和输人脉冲的时间关系,可以用一个时序图把两个脉冲对准,从而使得这些脉冲边沿的发生以正确的时间关系展现出来。输入脉冲的上升沿和输出脉冲的下降沿在相同的时间出现(理想状态)。类似地,输入脉冲的下降沿和输出脉冲的上升沿在相同的时间出现(理想状态)。这种时序关系如图3.3所示。实际上,从输入的变化到输出的变化有一个非常小的延迟。时序图在说明具有多个脉冲的数字波形之间的时间关系时特别有用。
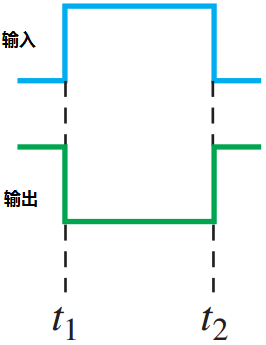 $$
图3.3~~~在图3.2条件下的时序图
$$
$$
图3.3~~~在图3.2条件下的时序图
$$
3.1.5 反相器的逻辑表达式
- ◇ 布尔代数使用变量和运算符来描述逻辑电路。
在布尔代数(它是逻辑电路的数学基础并且将在第4章得到全面的介绍)中,变量可以由多个字母表示,但是通常由一个或两个字母表示。接近字母表中开始位置的通常表示输人,而接近结束位置的通常表示输出。变量的反码由字母上方的横杠来表示。变量可取的值是 1 或者 0。如果一个变量是 1,它的反码就是 0,反之亦然。
反相器(非门电路)的运算可以用下面的方式表示: 如果输入变量为 A,输出变量为 X,那么 $$ X=\overline{A} $$ 这个表达式说明输出是输入的反码,所以如果 A=0,那么 X =1; 而如果 A=1,那么 X =0。图3.6给出了这种情况。反变量 A 可以读做 A 杠或者 A 反。
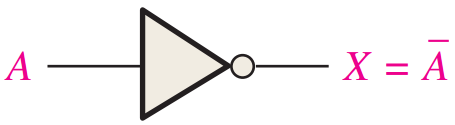 $$
图3.6~~~反相器对输入变量求反
$$
$$
图3.6~~~反相器对输入变量求反
$$
3.1.6 应用举例
图3.7给出了一个产生 8 位二进制数反码的电路。二进制数的位被加到反相器的输入上,二进制数的反码出现在输出中。
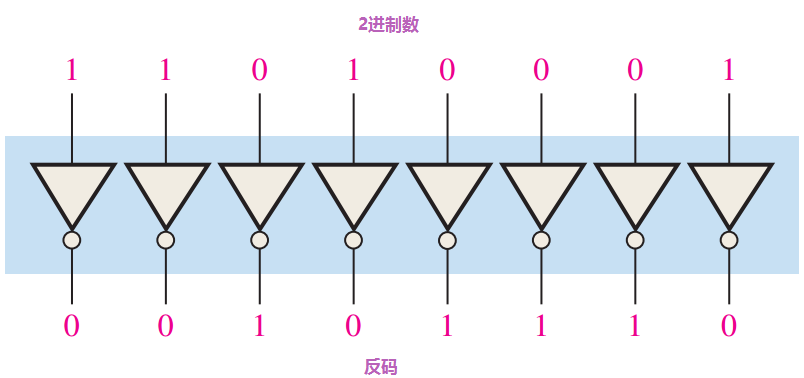 $$
图3.7~~~使用反相器的反码电路举例
$$
$$
图3.7~~~使用反相器的反码电路举例
$$